Container's Charateristics

Spatial provides 8 different containers, with the following characteristics:

spatial::point_multiset containers will store objects in any given number of dimensions, the value type value_type is also used as the key and it is stricly equivalent to key_type. It is also immutable.
spatial::point_multimap containers will store a pair of key and mapped types in any given number of dimension, the key type key_type is immutable, while the mapped_type can be mutated. value_type is made of std::pair<key_type, mapped_type>.
spatial::box_multiset and spatial::box_multimap have similar differences as presented above, additionally, the number of dimension used in this container have to be even: 2, 4, 6, 8, etc.
spatial::idle_point_multiset, spatial::idle_box_multiset, spatial::idle_point_multimap and spatial::idle_box_multimap have similar difference as presented above, however the are not automatically rebalancing. To obtain a perfectly balanced tree, the user of the library must call the function rebalance(), which is only found in these containers.

In addition to the differences above, all container share the same following properties:

They store value_types in memory, always.
They store arbitrary value_type, provided that value_compare can compare 2 distinct value types along the same dimension. See Trivial Comparison Concept.
The only necessary requirements on key_type and value_type is that they must be copy-constructible.
Currently, all the containers in the library are stable: once a value_type has been inserted in the container, its location in memory will not change, regardless of insertion or removal taking place the container. That means you can retain an iterator on an element of the container for as long as the container exists and as this element is not being removed from the container. Example: std::vector is not a stable container, while std::list is a stable container.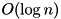
Not only are all containers stable, but so long as data are not modified in the containers, the containers are re-entrant. This means you can create multiple threads with thread-local iterators or algorithms working on the containers.
Currently all containers closely mimic the STL Standard Associative Container in functionalities and performance, with insertion and removal complexity close to $O(\log n)\,$ . Their iterators are bidirectional iterators and can be used in general STL algorithms. They are some notable differences: currently the Spatial containers do not provide a range erase function (and maybe, never will).

If you are wondering which containers to use for which situation, the Quick Starting Guide provides an small guide to answer this question.

Container's Interface

All containers in the library have the following generic interface:

Member Function	Description	Complexity
`iterator insert(const value_type& value)`	Insert a `value_type` `value` into the container. The `value` will be copied to its final memory destination in the container.	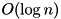$O(\log n)\,$
`template <typename Iterator> void insert(Iterator first, Iterator last)`	Insert a sequence of value in the container. `Iterator` should be a forward iterator.	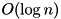$O(\log n)\,$ for each inserted elements
`iterator find(const value_type& value) const_iterator find(const value_type& value) const`	Returns an iterator pointing to the one of the values that compare equivalently to `value`. If no value compares equivalently to `value`, `end()` is returned.	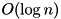$O(\log n)\,$
`iterator begin() const_iterator begin() const iterator end() const_iterator end() const`	Returns an iterator pointing to the beginning of the container for `begin()` and past-the-end for `end()`. This iterator can be used to iterate through all elements in the container.	$O(1)\,$
`std::size_t erase(const value_type& value)`	Erase all values in the container that compare equivalently to `value`. Returns the number of values that where erased.	$O(n^{1\,-\,1/d})\,$ for each erased element
`void std::size_t erase(iterator iter)`	Erase the value pointed to by `iter` in the container.	$O(n^{1\,-\,1/d})\,$

See each individual container for a more details explanation of their detailed interface: