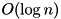Functions with fractional time complexity in dimension 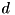 noted
noted  will run and return their output in an amount of time that depends primarily on the number of dimensions used in the container.
will run and return their output in an amount of time that depends primarily on the number of dimensions used in the container.
Proper balancing of the tree and choice of dimension for the search will also affect the running time of the function, but it has less influence as the number of elements in the container increases.
Function of this time complexity will amortize overtime, however they will not amortize as fast as logarithmic time complexity function. And therefore, for the benefit of amortization to show, it is often necessary that for a given dimension 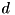 and number of elements
and number of elements 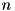 in the tree, the number of elements in the tree be far superior the exponent of the dimension:
in the tree, the number of elements in the tree be far superior the exponent of the dimension:
![\[n > 2^{d\,+\,1}\]](form_4.png)
This class of time complexity is very common on many of the function of the containers based on a k-d tree. This is due to the invarient of the k-d tree that acts on a single dimension at every depth of the k-d tree. Thus, if a point is being searched for in a particular dimension, and the space has 3 dimensions to work with, then prunning (i.e. eleminating part of tree from the search) only happens once every 3 steps down. By comparison, in a regular binary search tree, prunning occurs at every step down.
To give an idea of how prunning will work with such kind of time complexity, the table below shows the number of node that will be prunned for a various ranks and for various number of elements, if the tree is perfectly balanced. The value below are only representative, to give an idea of the evolution of the running time for a function of such complexity. The number of nodes visited versus nodes prunned by an algorithm is generally one of the most reliable indicator of the running time of a function in a tree.
| Number of elements in the container | Number of dimension = 1: 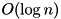 | Number of dimension = 2:  | Number of dimension = 3:  | Number of dimension = 4:  |
| nodes visited | node prunned | nodes visited | node prunned | nodes visited | node prunned | nodes visited | node prunned |
| 16 | 4 | 12 | 8 | 8 | 8 | 8 | 9 | 7 |
| 64 | 6 | 58 | 17 | 47 | 27 | 37 | 31 | 33 |
| 256 | 8 | 248 | 35 | 221 | 76 | 180 | 103 | 153 |
| 1024 | 10 | 1014 | 67 | 957 | 203 | 821 | 322 | 702 |
| 4096 | 12 | 4084 | 140 | 3956 | 525 | 3571 | 970 | 3126 |
| 16384 | 14 | 16370 | 281 | 16103 | 1339 | 15045 | 2852 | 13532 |
| 65536 | 16 | 65520 | 537 | 64999 | 3394 | 62142 | 8265 | 57271 |
| 262144 | 18 | 262126 | 1126 | 261018 | 8576 | 253568 | 23729 | 238415 |
| 1048576 | 20 | 1048556 | 2252 | 1046324 | 21643 | 1026933 | 67744 | 980832 |
| 4194304 | 22 | 4194282 | 4300 | 4190004 | 54579 | 4139725 | 192729 | 4001575 |
| 16777216 | 24 | 16777192 | 9011 | 16768205 | 137576 | 16639640 | 547113 | 16230103 |
| 67108864 | 26 | 67108838 | 18022 | 67090842 | 346732 | 66762132 | 1551018 | 65557846 |
| 268435456 | 28 | 268435428 | 34406 | 268401050 | 873793 | 267561663 | 4393263 | 264042193 |
As can be seen from the table above, for a single dimension, the number of node prunned by an algorithm running in logarithmic amortized time becomes larger than the number of node visited even when just a few nodes are in the tree. For space of 4 dimensions, we need to insert around 200 points in order to count more node prunned than nodes visited.
In practices, because tree does not have a very good locality of reference, iterating through very large trees is further slown down by the number of cache misses. If your application depends heavily on a function that runs in fractional time complexity in a high number dimensions (i.e. above 10 for example), and you do not plan to have a very large number of elements in your tree (i.e. less 10,000 for example), containers in this library may not be the most optimized solution for you, and you may need to look at other advanced solutions. In some cases, a std::vector<> may even provide better raw performance.
- Member spatial::details::decrement_mapping (NodePtr node, dimension_type dim, Rank rank, dimension_type map, KeyCompare key_comp)
- This function has average fractional time complexity:

- Member spatial::details::decrement_ordered (ordered_iterator< Container > &iter)
- This function has average fractional time complexity:

- Member spatial::details::increment_mapping (NodePtr node, dimension_type dim, Rank rank, dimension_type map, KeyCompare key_comp)
- This function has average fractional time complexity:

- Member spatial::details::increment_ordered (ordered_iterator< Container > &iter)
- This function has average fractional time complexity:

- Member spatial::details::Kdtree< Rank, Key, Value, Compare, Alloc >::find (const key_type &key)
- This function has average fractional time complexity:

- Parameters
-
| key | the value to be searched for. |
- Returns
- An iterator to that value or an iterator to the element past the end of the container.
- Member spatial::details::lower_bound_mapping (NodePtr node, dimension_type dim, Rank rank, dimension_type map, KeyCompare key_comp, const KeyType &bound)
- This function has average fractional time complexity:

- Member spatial::details::lower_bound_ordered (ordered_iterator< Container > &iter, const typename container_traits< Container >::key_type &bound)
- This function has average fractional time complexity:

- Member spatial::details::maximum_mapping (NodePtr node, dimension_type dim, Rank rank, dimension_type map, KeyCompare key_comp)
- This function has average fractional time complexity:

- Member spatial::details::maximum_ordered (ordered_iterator< Container > &iter)
- This function has average fractional time complexity:

- Member spatial::details::minimum_mapping (NodePtr node, dimension_type dim, Rank rank, dimension_type map, KeyCompare key_comp)
- This function has average fractional time complexity:

- Member spatial::details::minimum_ordered (ordered_iterator< Container > &iter)
- This function has average fractional time complexity:

- Member spatial::details::upper_bound_mapping (NodePtr node, dimension_type dim, Rank rank, dimension_type map, KeyCompare key_comp, const KeyType &bound)
- This function has average fractional time complexity:

- Member spatial::details::upper_bound_ordered (ordered_iterator< Container > &iter, const typename container_traits< Container >::key_type &bound)
- This function has average fractional time complexity:

- Member spatial::mapping_begin (Container &container, dimension_type mapping_dim)
- This function has average fractional time complexity:

- Member spatial::mapping_lower_bound (Container &container, dimension_type mapping_dim, const typename container_traits< Container >::key_type &bound)
- This function has average fractional time complexity:

- Member spatial::mapping_range (const Container &container, dimension_type mapping_dim)
- This function has average fractional time complexity:

- Member spatial::mapping_range (Container &container, dimension_type mapping_dim)
- This function has average fractional time complexity:

- Member spatial::mapping_upper_bound (Container &container, dimension_type mapping_dim, const typename container_traits< Container >::key_type &bound)
- This function has average fractional time complexity:

- Member spatial::ordered_begin (const Container &container)
- This function has average fractional time complexity:

- Member spatial::ordered_begin (Container &container)
- This function has average fractional time complexity:

- Member spatial::ordered_lower_bound (const Container &container, const typename container_traits< Container >::key_type &bound)
- This function has average fractional time complexity:

- Member spatial::ordered_lower_bound (Container &container, const typename container_traits< Container >::key_type &bound)
- This function has average fractional time complexity:

- Member spatial::ordered_range (const Container &container)
- This function has average fractional time complexity:

- Member spatial::ordered_range (Container &container)
- This function has average fractional time complexity:

- Member spatial::ordered_upper_bound (Container &container, const typename container_traits< Container >::key_type &bound)
- This function has average fractional time complexity:

- See also
- ordered_iterator
- Member spatial::ordered_upper_bound (const Container &container, const typename container_traits< Container >::key_type &bound)
- This function has average fractional time complexity:

- See also
- ordered_iterator

 noted
noted  will run and return their output in an amount of time that depends primarily on the number of dimensions used in the container.
will run and return their output in an amount of time that depends primarily on the number of dimensions used in the container.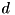 and number of elements
and number of elements 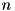 in the tree, the number of elements in the tree be far superior the exponent of the dimension:
in the tree, the number of elements in the tree be far superior the exponent of the dimension:![\[n > 2^{d\,+\,1}\]](form_4.png)