 |
Spatial C++ Library
Generic Multi-Dimensional Containers and Spatial Operations
|
 |
Spatial C++ Library
Generic Multi-Dimensional Containers and Spatial Operations
|
| ▼User Manual | |
| Installing the Library | The installation details are presented in the INSTALL file that is provided in the top directory of the source packages |
| Compiling the Unit Tests and the Examples | |
| ▼Structure of the Library | |
| Containers | |
| Iterators and Queries | Iterators are used in Spatial to perform all types of query in the container that can return a range of elements |
| Functionals | |
| ▼Concepts | |
| Link Mode | A Link Mode defines the relationship between a node and the links that bear the node |
| Trivial Comparison | This concept defines the model for a functor class used to perform strict comparison between two values of a spatial container, over a single dimension |
| Generalized Comparison | Generalized comparison concept defines the model for a functor used to perform a strict comparison between two values of a spatial container, over the same or a different dimension |
| Region Predicate | This concept defines the requirements for a predicate to be used in region queries |
| Metric | This concept defines the requirements for a Metric to be used with spatial::neighbor_iterator |
| Difference | This concept defines the requirements for objects to be used in nearest neighbor queries with the library's built-in metrics such as spatial::euclidian, spatial::quadrance or spatial::manhattan |
| ▼Complexity in the Library | |
| Constant Time Complexity | Functions with constant time complexity, noted 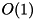 , will run and return their output in very similar amounts of time regardless of any other factors, such as number of elements in a container, size of a range evaluated, etc , will run and return their output in very similar amounts of time regardless of any other factors, such as number of elements in a container, size of a range evaluated, etc |
| Fractional Time Complexity | Functions with fractional time complexity in dimension 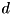 noted noted 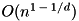 will run and return their output in an amount of time that depends primarily on the number of dimensions used in the container will run and return their output in an amount of time that depends primarily on the number of dimensions used in the container |
| Quasilinear Time Complexity | Functions with quasilinear time complexity, noted 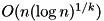 will return their output in an amount of time mostly proportional to the number of elements being considered, although their running time will still grow faster than pure linear time complexity, however it is still very close to it will return their output in an amount of time mostly proportional to the number of elements being considered, although their running time will still grow faster than pure linear time complexity, however it is still very close to it |
| Linear Time Complexity | Functions with linear time complexity, noted 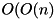 , will return their output in an amount of time proportional to the number of element in the tree , will return their output in an amount of time proportional to the number of element in the tree |
| Logarithmic Time Complexity | Functions with logarithmic time complexity, noted 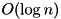 will run and return their output in an amount of time that depends only on the number of elements in the tree will run and return their output in an amount of time that depends only on the number of elements in the tree |
| ▼Performance of the library | |
| Insertion Performance | To be completed |